gruposanguineo<-factor(c("A","B","A","AB","A","O","A","B","A"),levels=c("A","B","AB","O"))
table(gruposanguineo)/length(table)gruposanguineo
A B AB O
5 2 1 1 4 Métodos descriptivos
En general, hay tres estrategias para sintetizar la información muestral: (1) La elaboración de tablas de frecuencias, (2) de diagramas de frecuencias y (3) el cálculo de medidas descriptivas. En lo que sigue, se va a suponer que el orden de obtención de los datos es irrelevante, es decir, que los datos no constituyen una serie con secuencia temporal.
La forma de resumir la información recogida en una variable está condicionada por el tipo que esta tenga; no será lo mismo resumir el contenido de una variable de tipo binario (como la presencia o no de cierta patología), que una de tipo cuantitativo (como el nivel de colesterol).
4.1 Tablas de frecuencias
Por tabla de frecuencias de una variable se entiende la presentación tabular de las categorías, o de los valores, que toma dicha variable y la frecuencia, o veces que se repiten, en la muestra. Cuando la variable es de tipo nominal, el orden de presentación de las categorías es irrelevante y se pueden definir dos tipos de frecuencias: las absolutas y las relativas.
En la Figura 4.1 se presenta la tabla de frecuencias de la variable grupo_sanguineo correspondiente a una muestra de \(n=500\) casos. Podemos denominar \(n(A)\) a la frecuencia absoluta de la categoría \(A\), es decir, al número de veces que se repite esta categoría de la variable. Normalmente, para hacer más operativa la alusión a las categorías, se suele utilizar una notación con subíndices, de manera que \(n_1, n_2,...\) aluden a las frecuencias absolutas de las categorías colocadas en primero, segundo,… lugar de la tabla, respectivamente. De forma genérica, es más habitual considerar la notación \(n_i\) para aludir a la frecuencia absoluta de la categoría \(i\)-ésima. La estandarización de la frecuencia relativa respecto al número total de observaciones, \(n\), es la frecuencia relativa, que podemos definir como \[f_i=\frac{n_i}{n}.\] Esta proporción es siempre un tanto por uno y al multiplicarla por 100 se convierte en un tanto por ciento. Una variable de tipo nominal no admite más frecuencias que las que se acaban de presentar, sin embargo, cuando aparece la relación de orden entre las categorías de la variable -es el caso de variables de tipo ordinal y de tipo cuantitativo-, es posible definir las frecuencias acumuladas. La frecuencia absoluta acumulada de una categoría representa el número de casos que corresponden a dicha categoría o a las anteriores a ella. Lo mismo es aplicable para las frecuencias relativas acumuladas, que para una categoría dada, representan la proporción de casos que pertenecen a ella o a las anteriores. En la Figura 4.2 se presentan estas frecuencias (las relativas en forma de porcentaje) y el procedimiento de cálculo. Así, por ejemplo, de esta tabla se deduce que el 56.4% de los casos no han mejorado (son los 282 casos incluidos en la categoría “igual” o en las anteriores).
Las variables cuantitativas de tipo discreto se pueden resumir de esta misma manera, pero siempre que la riqueza de valores distintos sea reducida. Cuando no es así, el tratamiento con las variables discretas es el mismo que con las de tipo continuo, se debe considerar una agrupación en intervalos. En la Figura 4.3 se presentan dos tablas descriptivas de la distribución de frecuencias de la variable edad tratada de forma discretizada. En la Figura 4.3 de la izquierda, los n=500 casos se distribuyen en k=6valores distintos de la edad, de manera que es posible especificar la frecuencia correspondiente a cada una de estas 6 clases. Sin embargo, en la Figura 4.4, los valores observados de la edad cubren un rango muy amplio (desde menos de 20 hasta màs de 40), y no sería una síntesis muy útil una tabla con tantas filas y frecuencias relativamente reducidas para cada valor. El recurso es agrupar la variable en intervalos y presentar las frecuencias con las que distribuyen los casos en esos intervalos.
Dos formas de resumir la variable edad cuando se trata de forma discreta.
La forma de elaborar los intervalos no es única, pero deben observarse ciertas reglas. Los intervalos deben ser (1) homogéneos, es decir, que todos tengan la misma amplitud (la amplitud es la diferencia entre los límites superior e inferior, en la tabla de la Figura 4.4, la amplitud de los cuatro intervalos centrales es de 4 años). Además, los intervalos deben ser (2) exhaustivos, es decir, que deben abarcar a todo el recorrido de la variable y (3) excluyentes, esto es que no pueden solaparse. Las dos últimas condiciones garantizan que cada observación esté incluida en uno, y solo uno, de los intervalos. Como veremos más adelante, es muy habitual que la distribución de una variable cuantitativa se densifique en una región más o menos central del recorrido de la variable y que las frecuencias decaigan por cada lado a medida que los valores se alejan de esta parte central. Se alude a las porciones extremas como las colas de la distribución. Para que una tabla de frecuencias sea un buen resumen de la distribución de las frecuencias observadas, debe de reproducir bien la presencia, o no, de esta estructura. Por ello, cuando aparecen pocos valores que resultan extremos, se recurre a intervalos como el primero y el último de la Figura 4.4. Se trata de evitar tener que indicar un número excesivo de intervalos con colas largas que presenten frecuencias muy bajas o incluso nulas. En cualquier caso, siempre debe primar el sentido común, una tabla de frecuencias es un resumen y el objetivo debe de ser hacer un buen resumen. También puede resultar llamativa una peculiaridad de la tabla de la Figura 4.4. Estrictamente hablando, los intervalos presentados no son exhaustivos, ya que hay un hueco de una unidad entre cada uno de ellos (del 21-25 se pasa al 26-30, y así con los demás). Esta forma de elaborar los intervalos pone de manifiesto que la variable, aunque sea de tipo continuo, se esta tratando de forma discretizada. Es decir, solo se consideran los valores enteros, no existen observaciones como 25.5 o 25.7. O son 25 o son 26 años. De lo contrario, hay que solapar los límites para cumplir con la exhaustividad, como ocurre en la tabla presentada en la Figura 4.5. En ella, la especificación de los intervalos se ha hecho con la notación matemática habitual para indicar si un intervalo es abierto (se indica con paréntesis y se traduce en que el límite no entra en el intervalo) o cerrado (indicado con corchete, ahora el límite sí que está incluido en el intervalo), de manera que, por ejemplo, el primer intervalo no contiene al valor 101 pero sí al 128.
La agrupación en intervalos invita a cuestionarse cuántos intervalos se deben hacer. Esto va a depender del recorrido de la variable y del tamaño muestral. Existen criterios, como el clásico de Sturges (1926), para calcular el número de intervalos, pero siempre debe primar el sentido común: muchos intervalos no resumen la distribución y pocos la resumen demasiado.
4.1.1 Procedimientos de R para obtener tablas de frecuencias
La función del sistema base para obtener la tabla de frecuencias de una variable es table(). Veamos algunos ejemplos, comenzando por considerar una variable de tipo nominal (factor)
la función table() devuelve una tabla con las categorías en la primera fila y las frecuencias correspondientes absolutas en la segunda. Aunque la variable no es ordinal, las categorías se ordenan según se ha especificado en el parámetro levels de la función factor(). Una situación análoga se da con las variables ordinales (definidas con ordered()).
estado<-ordered(c("igual","igual","peor","mejor","peor","igual","mejor","igual","mejor","mejor"),levels=c("peor","igual","mejor"))
table(estado)estado
peor igual mejor
2 4 4 En el caso de variables cuantitativas, cuando la variable es discreta y su recorrido (número de valores distintos) es limitado, la tabulación mediante table() sigue siendo de utilidad:
diasingreso<-c(1,3,2,1,5,6,4,3,1,4)
table(diasingreso)diasingreso
1 2 3 4 5 6
3 1 2 2 1 1 Sin embargo, table() no hace ningún tipo de agrupación en intervalos, por lo que su interés es limitado cuando la variable presenta cierta riqueza de valores distintos, como es el caso de las continuas:
# para una variable continua
calcio<-c(9.8,9.5,8.7,10.2,9.3,9.6,8.9,10.4,9.9,10.2)
table(calcio)calcio
8.7 8.9 9.3 9.5 9.6 9.8 9.9 10.2 10.4
1 1 1 1 1 1 1 2 1 Con table() tampoco es posible obtener directamente otro tipo de frecuencias, tales como las relativas o las acumuladas.
BioestadísticaR impementa la función freq() para facilitar la creación de tablas de frecuencias más elaboradas. Además de la frecuencia absoluta, freq() proporciona la relativa y la relativa acumulada, automatizando la agrupación en intervalos si es que la variable hace esto necesario. La sintaxis completa de freq() es la siguiente:
freq(x = NULL, acum = TRUE, cuts = 0, agrup = TRUE, decs = 3, grf = TRUE)
xvector de datos a tabularacumvalor lógico indica si se muestran (TRUE) o no (FALSE) las frecuencias acumuladas. El valor por defecto esTRUEcutspermite modificar el número de intervalos. Si se omite y la variable tiene más de 10 valores distintos, se usa el criterio de Sturges.agrupes un valor lógico. Si se estableceagrup = FALSE, no se hace agrupación en intervalos aunque la variable tenga más de 10 valores diferentes.grfes un valor lógico que condiciona si se presenta una salida gráfica (por defecto esTRUE) el tipo de diagrama lo establece el tipo de la variable y su riqueza de valores distintos.
Veamos un ejemplo:
estado <- ordered(c("igual","igual","peor","igual","peor","igual","mejor","igual","mejor","mejor"),levels=c("peor","igual","mejor"))
BioestadisticaR2::freq(estado, grf=FALSE)
Distribución de frecuencias
--------------------------------
Variable: estado
n= 10
x Freq Prop Prop.Acum
1 peor 2 0.2 0.2
2 igual 5 0.5 0.7
3 mejor 3 0.3 1.0La función freq() se ha invocado anteponiendo el nombre del paquete BioestadisticaR2 separando con :: el nombre de la función. Esta sintáxis le indica a R donde en qué paquete está la función freq(). Se puede obviar esta sintaxis si cargamos previamente la librería (mediante el panel de paquetes de RStudio o bien escribiendo en la consola library(BioestadisticaR2)). En adelante se usará siempre la sintaxis BioestadisticaR2::función para distinguir claramente entre las funciones que corresponden al paquete y las del lenguaje base (sin prefijo). Se ha indicado grf=FALSE para no alargar este documento, si deja esta opción en TRUE podrá ver el diagrama resultante en el panel de gráficos de RStudio.
4.2 Diagramas de frecuencias
Por diagrama de frecuencias de una variable se entiende una representación gráfica en la que se plasman las categorías o los valores de la variable, y la frecuencia con que estas aparecen en la muestra. El criterio que deben mantener este tipo de diagramas es que el motivo gráfico asignado a cada categoría debe ser igual o proporcional a su frecuencia. Las frecuencias consideradas pueden ser las absolutas o las relativas (esto no cambiará la apariencia global del gráfico). Cuando la métrica de la variable sea ordinal o cuantitativa, se pueden considerar también las frecuencias acumuladas, para dar lugar a los diagramas acumulativos.
El tipo o métrica de la variable también impone qué diagramas van a ser apropiados, o no, para representarla. El la Figura 4.6 se resumen los tipos básicos de diagramas de frecuencias y los tipos de variable en que resultan adecuados.
Diagrama de sectores. Este tipo de diagramas debería ser usado solamente en el caso en que la variable representada sea de tipo cualitativo, ya que la relación ordinal no queda bien representada. El motivo gráfico asignado a cada categoría es el área de un sector de circunferencia. Como este área queda determinada por el ángulo \(\alpha\) que defina el sector, basta considerar el producto entre los grados totales de la circunferencia y la frecuencia relativa de cada categoría para obtener el ángulo que le corresponde a la misma: \[ \alpha_i = 360 \frac{f_i}{n}\] Diagrama de barras. Se trata de una representación en un sistema de ejes cartesianos en donde a cada categoría de la variable se le asigna una barra cuya altura es igual o proporcional a la frecuencia con que se repite en la muestra. En estos diagramas, la anchura de la barra es irrelevante (aunque debe ser la misma para todas las barras). Estos diagramas sí que permiten reproducir la relación ordinal entre las categorías, de manera que son adecuados para variables categóricas, ordinales y cuantitativas discretas. Cuando las cuantitativas presentan mucha variedad de valores distintos (imitando a las continuas) normalmente es preferible utilizar el histograma para representarlas.
La representación puede hacerse considerando en el eje de abscisas a la variable y en el de ordenadas a la frecuencia, o al revés.
Una variante de estos diagramas son los diagramas de Pareto. Se trata de diagramas de barras en los que las categorías de la variable se ordenan de acuerdo a su frecuencia, lo que permite destacar la relevancia progresiva de las categorías. Como esta ordenación alterará la impuesta por la posible relación ordinal entre las categorías, el diagrama resulta adecuado solamente para variables de tipo cualitativo.
Polígonos de frecuencias. Apropiados para variables con relación ordinal y en especial variables de tipo continuo. Se trata de una representación en un sistema de ejes cartesianos en donde los valores de la variable se disponen en el eje de abscisas y los de la frecuencia en el de ordenadas. Para cada valor de la abscisa, se localiza el punto de la ordenada relativo a la frecuencia correspondiente y finalmente se unen todos los puntos formando una línea poligonal. El hecho de que se unan los puntos mediante una línea genera una sensación de continuidad, de transición de un valor al siguiente, por lo que este tipo de representación es más adecuado para variables continuas.
De especial interés para representar los valores que toma una variable observada en el tiempo, denominándose entonces gráfico temporal.
Histograma. Se trata de la representación adecuada para variables continuas o discretas que presenten mucha riqueza de valores distintos (imitando la continuidad). Para construir un histograma, el primer paso es agrupar los valores de la variable en intervalos homogéneos. El motivo gráfico asignado a cada intervalo es un rectángulo con un área proporcional a la frecuencia correspondiente a dicho intervalo. La homogeneidad de los intervalos se traduce en que todos los rectángulos van a tener la misma base, con lo que bastará con hacer que su altura sea proporcional a la frecuencia. Como ocurre con el diagrama de barras, en un histograma se pueden disponer los valores de la variable (los intervalos) en el eje de abscisas (es lo más habitual) o en el de ordenadas, generando una imagen rotada 90º respecto a la anterior.
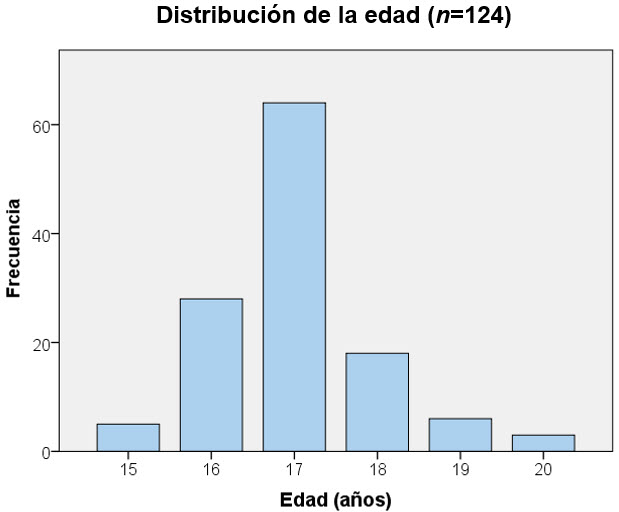
Conviene destacar la principal diferencia entre un diagrama de barras y un histograma. Como ya se ha indicado, en el primero, la anchura de la barra es irrelevante, es una cuestión de estética, en lugar de una barra se podría dibujar una línea. La idea es que las barras no se solapan, hay un “hueco” entre una barra y la siguiente, poniendo de manifiesto la falta de continuidad entre las categorías o los valores representados. En la Figura 4.7 no hay nadie con edades intermedias entre 15 y 16 años, por ejemplo. Sin embargo, en el histograma, el punto donde acaba un intervalo constituye el comienzo del siguiente, de manera que los rectángulos asignados a cada intervalo sí que se solapan, tal y como se pone de manifiesto en la Figura 4.8.
4.2.1 Diagramas de frecuencias con el sistema base de R
A continuación se indican los procedimientos del sistema base para obtener diagramas de frecuencias con R. Más adelante se verá una opción mejor, que es el uso del potente paquete gráfico ggplot2. La web R Charts presenta una amplia documentación sobre la generación de gráficos con R, tanto a través del sistema base como a través del potente paquete gráfico ggplot2.
Funciones del sistema base para generar diagrmas de frecuencias
pie(table(factor))diagrama de sectores.barplot(table(factor o variable discreta))diagrama de barras.
Las funciones anteriores operan sobre el resultado de la función table(), que es la encargada de determinar las frecuencias de cada categoría.
hist(variable)histograma.boxplot(variable, factor)diagrama de cajas. Si se indica un factor (es optativo), la variable se representa para cada nivel del factor.
4.3 Medidas descriptivas
Por medidas descriptivas, o medidas de síntesis, debemos entender ciertos indicadores que son obtenidos a partir de los datos muestrales y que caracterizan aspectos de su distribución tales como su posición, su dispersión y su forma. En primera instancia, el tipo que tenga la variable condiciona qué medidas descriptivas se pueden calcular. En el caso de variables cualitativas la síntesis no suele ir más allá de la indicación de las frecuencias relativas de cada modalidad, posiblemente destacando qué clase tiene mayor frecuencia (la moda). Cuando se trata de variables de tipo ordinal, la posición y dispersión de la distribución se puede sintetizar con los denominados estadísticos de orden (como son la mediana, los percentiles y el rango intercuartílico que se verán a continuación). Pero es frecuente que al tratar con variables dicotómicas y también con las ordinales, se realice algún tipo de asignación numérica arbitraria y manejar medidas sintéticas propias de las variables de tipo cuantitativo. Veamos a continuación algunas de las medidas de síntesis más habituales en Ciencias de la Salud.
4.3.1 Medidas de posición
Las medidas de posición son indicadores que sintetizan donde se sitúa la distribución. Esta caracterización se puede hacer aludiendo a su centro o bien a una porción extrema, de manera que se habla de medidas de posición con tendencia central (estas son la moda, la mediana y la media) y medidas con tendencia no central (los percentiles).
4.3.1.1 Moda
La moda muestral (\(Mo\)) de una variable es la categoría, o el valor, que aparece con mayor frecuencia en la muestra. Es una medida válida para variables de cualquier tipo, pero su interés a nivel inferencial es muy limitado, ya que no está garantizado que sea un solo valor; dos o más modalidades diferentes pueden aparecer con la misma frecuencia.
4.3.1.2 Mediana
La mediana de una variable en una muestra (\(Me\)) se define como la categoría -si la variable es ordinal- o el valor de la variable -si es numérica- que divide a la muestra ordenada en dos partes iguales, dejando al mismo número de observaciones por debajo y por encima de ella. Debe enfatizarse la relevancia de que los datos sean ordenables, es decir, deben ser de tipo ordinal o de tipo cuantitativo. El cálculo práctico se hace como sigue: para una muestra ordenada de tamaño \(n\), se determina la posición de la mediana que viene dada por la cantidad \(\frac{n+1}{2}\). Si el tamaño muestral es impar, la posición de la mediana será un valor entero y la mediana es el valor de la variable que ocupe esa posición central. Si el tamaño de muestra es par, al sumarle 1 se convierte en impar y al dividir por dos siempre será un valor entero más 5 décimas. Entonces la mediana se obtiene como la media aritmética entre los dos valores enteros centrales. En este caso, la mediana no tiene por qué ser un valor observado en la muestra. Cuando los datos muestrales están tabulados en forma de tabla de frecuencias, la mediana es el primer valor de la variable cuya frecuencia absoluta acumulada sea superior o igual a \(\frac{n+1}{2}\) o, equivalentemente, cuya frecuencia relativa acumulada sea mayor o igual a 0.5 (el 50% si se expresa como porcentaje). La definición de mediana se puede formalizar de acuerdo a la siguiente expresión \[Me=x_{(\frac{n+1}{2})}. \tag{4.1}\] El paréntesis del subíndice indica que la muestra está ordenada (\(x_1\) alude al primer valor observado y \(x_{(1)}\) al primer valor de la muestra ordenada, es decir, al mínimo).
Ejemplos del cálculo de la mediana
- Muestra 1: {10,15,18,25,27}, \(n=5\), posición mediana \(=\frac{5+1}{2}=3\), \(Me= 18\) (valor de la muestra ordenada que ocupa la posición 3)
- Muestra 2: {10,15,18,25,27,32}, \(n=6\), posición mediana \(=\frac{6+1}{2}=3.5\), \(Me=\frac{18+25}{2}=21.5\) (promedio entre los valores de la muestra ordenada que ocupan las posiciones 3ª y 4ª)
- Muestra de la Figura 4.2: La categoría mediana es
igual, lo que se interpreta diciendo que la mitad de los casos quedan igual o empeoran y la otra mitad quedan igual o mejoran. - Muestra de la Figura 4.3: \(Me=17\) años por ser este el primer valor de la variable cuyo porcentaje relativo acumulado supera el 50%.
- Muestra de la Figura 4.4: el intervalo mediano es el 26-30. Mediante interpolación lineal se puede aproximar el valor puntual de la mediana, pero la tabla de frecuencias es un resumen de los datos, las medidas descriptivas deben de obtenerse de los datos originales, no de una síntesis.
4.3.1.3 Media
Bajo el concepto de media se definen una familia de medidas de posición con tendencia central. La más habitual es la media aritmética, que se obtiene como la suma de los valores observados dividida por el número de observaciones: \[\bar x = \frac{1}{n}\sum\limits_{i = 1}^n {{x_i}} \tag{4.2}\] Obviamente, esta medida solo puede definirse cuando los datos son cuantitativos, aunque, como ya se ha señalado, la asignación de valores numéricos a variables dicotómicas y ordinales es una práctica frecuente y permite utilizar la media aritmética para localizar la distribución.
Otros tipos de media
Dada una muestra de valores \((x_1,x_2,\dots,x_n)\), el concepto de media se puede generalizar de acuerdo a la expresión de Foster:
\[\begin{equation*} M_m= \left\{ \begin{aligned} &\left( \frac{1}{n}\sum_{i=1}^{n}{x_i^m}\right)^{\frac{1}{m}} & \text{ si } m\neq 0 \\ &\left( \prod_{i=1}^{n}{x_i} \right)^\frac{1}{n} & \text{ si } m = 0 \end{aligned} \right. \end{equation*} \tag{4.3}\]
Es inmediato comprobar que si \(m=1\), se tiene \(M_1\), que es la media aritmética definida en la Ecuación 4.2. Otras medias posibles se adaptan a este formato al considerar diferentes valores de \(m\)
- Si \(m=2\), \(M_2\) es la media cuadrática \[M_2=\;\;Q=\frac{1}{n}\sum_{i=1}^{n}{x_i^2}.\] Constituye una estrategia útil para promediar cantidades que puedan presentarse con signos positivos y negativos pero lo que interesa es la magnitud en sí. Al elevar los valores al cuadrado, se elimina el signo, y el promedio resultante alude al de la magnitud. Esta forma de promediar se presentará más adelante, al definir la desviación típica.
- Si \(m=0\), \(M_0\) es la media geométrica \[M_0=\;\;G=\sqrt[n]{\prod_{i=1}^{n}{x_i}}.\] Este tipo de media es más conveniente que la aritmética cuando los valores aumentan en progresión geométrica. En Molina (2023) puede verse un ejemplo de su aplicación a las Ciencias de la Salud.
- Si \(m=-1\), \(M_{-1}\) es la media armónica \[M_{-1}=\;\;H=\frac{1}{\sum_{i=1}^{n}{\frac{1}{ x_i}}}.\] Es el recíproco de la aritmética. Una de sus aplicaciones es el promedio de velocidades. Molina (2022) es también una lectura recomendable para entender esta medida. Se aplica sobre cantidades mayores a cero (obsérvese que los cocientes no pueden tener como denominador al valor cero).
Para una muestra dada, se verifica que \(H\le G \le \bar{x} \le Q\).
En ocasiones, los valores a promediar pueden no tener la misma importancia relativa, unos “pesan” más que otros conforme a algún criterio preestablecido. En estos casos, se debe incluir el factor de ponderación \(w_i\) de cada observación \(x_i\) para obtener así la media ponderada \[\bar{x}_p = \frac{\sum\limits_{i = 1}^n {{w_i x_i}}}{\sum\limits_{i = 1}^n {{w_i}}} . \tag{4.4}\]
Ejemplos de media ponderada
En un curso académico se consideran las calificaciones siguientes: 6 en una asignatura de 3 créditos , 5 en otra de 3 créditos y 9 en una asignatura de 6 créditos. La media aritmética de las calificaciones es \(\bar{x}=\frac{6+5+9}{3}=6.67\), pero este promedio no es correcto, ya que la tercera asignatura tiene el doble de carga docente que las dos primeras. Los créditos de cada asignatura constituyen el peso o factor de ponderación de cada calificación: \(w_1=w_2=3\) y \(w_3=6\), de manera que la media ponderada será \[\bar{x}_p=\frac{3\cdot 6+ 3\cdot 5 + 6\cdot 9}{3+3+6}=7.25\] que es un promedio más justo que el anterior.
Cálculo de la media de una variable discreta resumida en una tabla de frecuencias. Para determinar la media aritmética de los datos presentados en la Figura 4.3 lo lógico es multiplicar cada valor de la edad (\(x_i\)) por su frecuencia (\(f_i\)): \[\overline{edad}=\frac{15\cdot 30+16\cdot 103+\dots+20\cdot 15}{30+103+\dots+15}=17.1.\] Aquí la frecuencia \(f_i\) actúa como factor de ponderación (el \(w_i\) de antes, la \(w\) alude a weight, peso en inglés), de manera que la expresión general para calcular la media de valores presentados en forma de tabla de frecuencias es \[\bar{x}=\frac{\sum_{i=1}^{n}{f_i\: x_i}}{\sum_{i=1}^{n}{f_i}}=\frac{\sum_{i=1}^{n}{f_i\: x_i}}{n}.\] Observemos que promediar los datos de la Figura 4.3 sumando los seis valores de edad y dividiendo por seis (el número de categorías) es una interpretación equivalente al primer planteamiento del ejemplo anterior, el de calcular la calificación media del curso sin considerar la carga docente de cada asignatura.
4.3.1.3.1 Mediana vs. media aritmética
A continuación, se destacan algunas diferencias entre la mediana y la media aritmética como medidas de posición con tendencia central.
Respecto a la métrica de la variable. Cuando los datos son de tipo ordinal ya se puede establecer la categoría mediana de las observaciones, no hace falta que sean valores numéricos, como requiere la media.
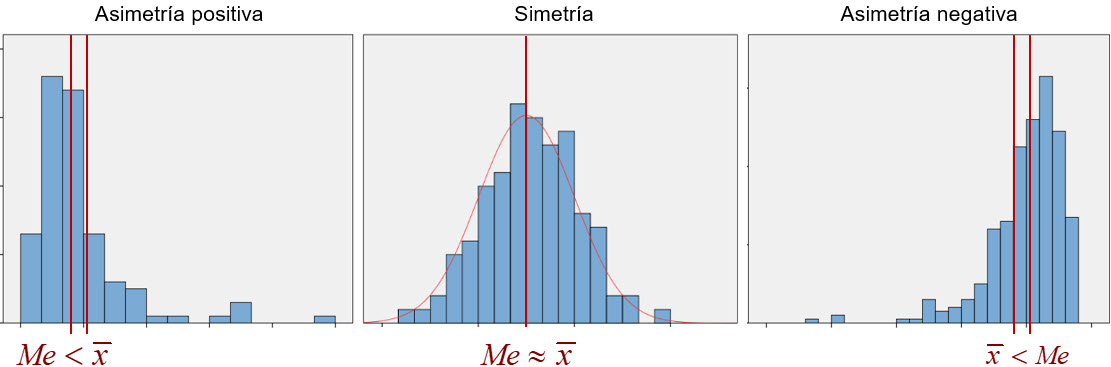
Criterio de centralidad. El criterio de centralidad de la mediana es que queden tantas observaciones por debajo como por encima de ella al presentar los datos de acuerdo con su relación de orden. Sin embargo, el criterio de centralidad de la media aritmética es que esta constituye el centro de gravedad de la distribución (Figura 4.9). Es decir, es el punto que hace mínima la suma de las distancias de todas las observaciones respecto a él, verificando que la suma de las distancias a las observaciones a su izquierda tiene la misma magnitud que la suma de las distancias a las observaciones a su derecha. Como consecuencia, a falta de más información, el mejor pronóstico para un nuevo valor, el que -en promedio- va a ser el más aproximado a la nueva observación, es el valor de la media aritmética. Esto confiere a la media un papel mucho más relevante en inferencia que el que tiene la mediana.
- Robustez. Cuando el tamaño muestral \(n\) es reducido, la media es una medida más sensible a la presencia de valores extremos (outliers en inglés) que la mediana, que se comporta de forma más robusta. Es decir, el valor de la media puede en presencia de valores extremos puede ser muy diferente al que se obtiene si se excluyen esos valores. Sin embargo, en la medida en que aumenta el tamaño muestral, la media va ganando robustez. Esta sensibilidad se pone de manifiesto en las distribuciones de la Figura 4.10. Cuando la distribución es simétrica, sus dos colas están equilibradas y la media y la mediana coinciden aproximadamente. Sin embargo, la falta de simetría provoca que el valor de la media cambie para compensar la presencia de valores extremos en una de las colas. Para la mediana es indiferente si una observación está alejada respecto al centro de la distribución, lo que cuenta solo es si está por encima o por debajo de ella.
4.3.1.4 Percentiles
Las medidas de posición consideradas hasta ahora se refieren a la posición central de la distribución conforme a algún criterio de centralidad. Pero también es de interés caracterizar la localización de los datos observados atendiendo a criterios no centrales. Los indicadores más inmediatos para localizar los extremos son el mínimo y el máximo. Obviamente, estos valores solo tienen sentido si los datos son de tipo ordinal o -sobre todo- numérico. Sin embargo, aunque la información que proporcionan es totalmente intuitiva, son indicadores dados por una sola observación, la extrema en cada sentido. Para caracterizar, de una forma más consistente, los extremos de la distribución es preferible hacerlo de forma más robusta, considerando indicadores que tengan implícita más información que la aportada por una sola observación. Estos indicadores son los percentiles. Se define el percentil alfa, \(P_\alpha\), como el valor de la variable que, en la muestra ordenada, deja por debajo de él al \(\alpha\cdot100\%\) de las observaciones. Es decir, al valor de la variable que, en la muestra ordenada, ocupa la posición \((n+1)\cdot\alpha\) \[P_\alpha=x_{\left( {(n+1)\cdot\alpha} \right)}. \tag{4.5}\] Esta definición es una generalización del concepto de mediana. Si en la Ecuación 4.5 consideramos \(\alpha=0.5\) se obtiene la Ecuación 4.1, por lo tanto \(Me=P_{0.5}\). Normalmente se alude a los percentiles con el valor de \(\alpha\) multiplicado por 100, de manera que la mediana es el percentil 50. Hay más percentiles con nombre propio. Los percentiles 25, 50 y 75 constituyen los tres cuartiles: \(Q1=P_{0.25}\), \(Q2=P_{0.50}\) y \(Q3=P_{0.75}\), que de forma conjunta permiten dividir a las observaciones en cuatro partes, cada una de las cuales contiene al 25% de los datos. Los nueve percentiles que de manera conjunta dividen a la muestra en 10 partes con el 10% de las observaciones son los deciles: \(D_1=P_{0.10}\),…,\(D_5=P_{0.50}=Me\),…,\(D_9=P_{0.90}\). En Ciencias de la Salud también se suelen considerar los dos terciles, que permiten fraccionar al conjunto de observaciones en tres partes, cada una con un 33.3% de ellas. De acuerdo a esta división, se categoriza la variable a valores bajos (si están por debajo del \(P_{0.33}\)), medios (si están comprendidos entre \(P_{0.33}\) y \(P_{0.66}\)) y altos (si están por encima de \(P_{0.66}\)).
Todos son cuantiles
Igual que los deciles “avanzan” acumulando fracciones del 10% y los cuartiles del 25%, el término percentil realmente alude a este tipo de indicadores que “avanzan” acumulando fracciones del 1%, de manera que, rigurosamente hablando, hay 99 percentiles que en conjunto dividen a la muestra en 100 partes, cada una con un 1% de las observaciones. El término genérico para todas estas medidas es el de cuantil. Por lo tanto, los percentiles, deciles, terciles, cuartiles,… son todos casos particulares de cuantiles. Sin embargo, en la literatura en Ciencias de la Salud está más extendida la denominación genérica de percentiles, en lugar de cuantiles, pudiendo abusar del término y hablar, por ejemplo, del percentil 97.5. En este texto se mantendrá este uso genérico del término percentil. Pero, cuidado, como se indicará más adelante, en lenguaje R la función para determinarlos es quantile().
El cálculo práctico de un percentil es similar al planteado en el cálculo de la mediana. Dado \(\alpha\) y una vez ordenada la muestra, se determina la posición \((n+1)\cdot\alpha\) y el valor de la variable que ocupa esa posición es el \(P_\alpha\). Lo que ocurre es que ahora el valor de la posición obtenido no será el intermedio entre dos posiciones concretas. Ahora, en lugar de calcular el promedio como en el caso de la mediana, lo correcto es interpolar. De esto se encargará el software adecuado. Sin embargo, sí que es práctico tener claro cómo determinar cierto percentil a la vista de una tabla de frecuencias. Si se dispone de las frecuencias relativas acumuladas, el \(P\alpha\) será el valor de la variable cuya frecuencia relativa acumulada sea la primera en superar el valor de \(\alpha\). Por ejemplo, en la tabla de la Figura 4.3, \(P_{17}=16\) años, ya que los \(15\) años solo acumulan el 6% de las observaciones. Análogamente, \(P_{50}=Me=17\) años y \(P_{95}=19\) años. La definición de percentil implica que dados dos valores \(\alpha_1<\alpha_2\), se tiene que \(P_{\alpha_1} \le P_{\alpha_2}\). Que la igualdad en esta expresión puede ocurrir, queda bien ilustrada con los datos de la tabla de la Figura 4.3. Por ejemplo, en ella se tiene que \(P_{30}=17\) años, pero también es \(P_{40}=17\) años. De hecho, todos los percentiles entre el 26.7 (\(P_{0.267}\)) y el 72.6 (\(P_{0.726}\)) son 17 años.
Es habitual caracterizar los extremos de una distribución mediante percentiles. Uno de los criterios más usados es el del 5%. De acuerdo con él, se considera como parte central de la distribución a la constituida por el 95% de los casos y como extremos al 5% repartido en las dos colas. Cuando la distribución es simétrica, lo lógico es que este 5% se reparta por igual, de manera que los límites quedan establecidos por los percentiles \(P_{0.025}\) y \(P_{0.975}\)
Conviene comentar que los percentiles empiezan a carecer de sentido cuando las muestras son pequeñas.
Los percentiles y el orden natural de la variable
4.3.2 Medidas de dispersión
Observemos las dos situaciones presentadas en la Figura 4.12. En los dos casos, la posición de la variable representada está caracterizada por la media, que resulta ser la misma en los dos grupos que aparecen en cada figura. Sin embargo, en ambas situaciones aparece una característica que permite diferenciar a los grupos: su dispersión o variabilidad.
Dada una muestra, del mismo modo que es posible caracterizar la posición de la distribución de la variable observada, también es posible caracterizar su dispersión. Se abordan a continuación los criterios y medidas que se utilizan para ello, debiendo tener presente que la variable considerada ha de ser de tipo numérico.
4.3.2.1 Rango o Amplitud
Se trata de la medida de dispersión más sencilla e inmediata. El rango (\(R\)), o amplitud (\(A\)), que queda definido como la diferencia entre el máximo y el mínimo de los valores de la variable \[R=x_{max} - x_{min}.\] Es una medida intuitiva y rápida de obtener, pero presenta el problema de que solo depende de dos observaciones, las dos extremas. Esto tiene dos implicaciones, por un lado, tal y como se ilustra en la Figura 4.13, no distingue entre una situación en donde el resto de las observaciones se reparten de forma homogénea entre los dos extremos (mayor variabilidad), de otra en la que todos los datos se agrupan en un intervalo reducido, dejando a uno, o a los dos extremos alejados de este grupo.
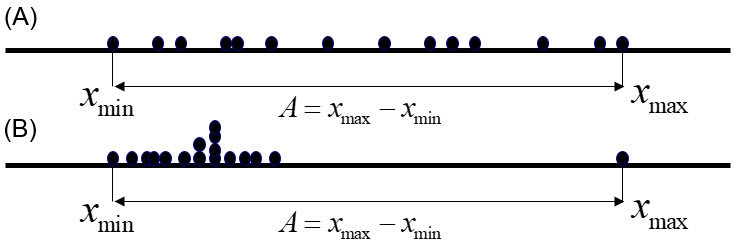
Por otro lado, es una medida muy sensible a la aparición de valores extremos. La aparición o no de este tipo de valores puede modificar sustancialmente el valor del rango.
4.3.2.2 Varianza
Al definir una medida descriptiva, lo ideal es que esta aproveche la información que aportan todos los datos observados, no solo la de los dos extremos, como hace el rango. Una buena forma de glosar la información aportada por toda la muestra es considerar el criterio de promedio. Pero para medir la dispersión, habrá que definir antes qué es lo que hay que promediar. Una posibilidad es establecer un valor de referencia y cuantificar las distancias1 de cada observación respecto a dicha referencia.
Lo más lógico es elegir como punto de referencia a una medida de posición con tendencia central, como la media aritmética o la mediana. Consideremos la media aritmética \(\bar{x}\). La dispersión \(d_i\) de una observación \(x_i\) respecto a la media se puede cuantificar por la distancia entre ambos valores, es decir \[d_i=x_i-\bar{x}\] Consecuentemente, la media aritmética de estas distancias es un buen candidato como medida de dispersión que tiene en cuenta la información de toda la muestra.
Sin embargo, surge una pega, la media de las distancias de cada observación a la media es siempre cero \[\bar{d}=\sum_{i=1}^{n}{\frac{d_i}{n}} = \sum_{i=1}^{n}{\frac{x_i-\bar{x}}{n}} =\sum_{i=1}^{n}{\frac{x_i}{n}}-\bar{x} = \bar{x}-\bar{x}=0.\] Esto es consecuencia del criterio de centralidad de la media aritmética, comentado en la Sección 4.3.1.3.1, la suma de las distancias a la media de las observaciones menores a esta medida es igual a la suma de las distancias de las observaciones mayores a la misma.\[\sum_{x_i<\bar{x}}{(x_i-\bar{x})}=-\sum_{x_i>\bar{x}}(x_i-\bar{x}).\] El problema radica en que el planteamiento no tiene en cuenta que las distancias no pueden ser negativas, algo que ocurre en la anterior definición siempre que se haga \(x_i-\bar{x}\) para valores \(x_i<\bar{x}\). La solución es considerar el cuadrado de estas diferencias, es decir, definir \[S^2=\sum_{i=1}^{n}{\frac{d_i^2}{n}}=\sum_{i=1}^{n}{\frac{(xi-\bar{x})^2}{n}}. \tag{4.6}\] Esta ya sí que es una buena medida de variabilidad, se denomina varianza y se puede definir como el promedio de las distancias al cuadrado de cada observación a la media. Solo queda un pequeño detalle. Cuando se considera esta varianza muestral para hacer inferencia sobre el valor de la varianza poblacional, este valor es sesgado, presenta una desviación respecto al verdadero valor poblacional (lo subestima), y este sesgo es más patente cuanto menor sea el tamaño muestral. La solución consiste en promediar las diferencias al cuadrado, no por el tamaño muestral \(n\), sino por los grados de libertad \(n-1\)
\[s^2=\sum_{i=1}^{n}{\frac{(xi-\bar{x})^2}{n-1}} \tag{4.7}\] Esta es la expresión insesgada de la varianza que se va a considerar en adelante. En algunos textos, se alude a esta expresión como cuasivarianza. Nosotros no lo haremos aquí, de acuerdo con otros autores, mantendremos el término varianza para aludir a ella, ya que es la expresión que se debe usar en inferencia. Es común aludir a la varianza cuyo denominador es \(n\) como varianza poblacional.
Qué son los grados de libertad
Tal y como expresa la Ecuación 4.7, la definición de la varianza incluye a toda la información muestral \((x_1,\dots,x_n)\) y a la aportada por la medida \(\bar{x}\). Pero en la obtención de \(\bar{x}\) ya se ha hecho uso de toda esa información muestral. Esto genera una ligadura o restricción. Veamos un ejemplo para entender esto mejor. Si consideramos la muestra \((4, 5, 12)\), se tiene que \(\bar{x}=(4+5+12)/3=7\). ¿Cuántos datos de esa muestra se pueden cambiar de forma que se mantenga \(\bar{x}=7\)?. Podemos comenzar sustituyendo arbitrariamente dos valores, por ejemplo, considerar el 6 y el 9, pero para que la media siga siendo 7, la tercera observación no puede tomar cualquier valor, ha de ser -forzosamente- otro 6 (\(\bar{x}=(6+9+x_3)/3=7\) solo si \(x_3=6\)). Mantener el valor de la media establece una restricción en los datos. Podríamos cambiar todos menos uno, que tendrá que tomar un valor concreto para mantener el de la media.
Esto supone que la información considerada en la Ecuación 4.7 es el valor que toma \(\bar{x}\) más los valores de \(n-1\) observaciones muestrales, no los de la muestra al completo, ya que la predeterminación de la media establece una restricción. Se dice entonces que se dispone de \(n-1\) grados de libertad. Es más conveniente que el denominador aluda a los grados de libertad (información real) que al tamaño muestral (información real más un dato redundante), ya se ha comentado que, en inferencia, la Ecuación 4.6 infravalora el valor de la varianza poblacional, siendo preferible la varianza expresada en la Ecuación 4.7.
4.3.2.3 Desviación típica
La varianza reúne la información de la dispersión de todos los valores observados en la muestra con un buen criterio de promedio. Pero esta información está expresada en las unidades de la variable elevadas al cuadrado. Si, por ejemplo, estamos estudiando la estatura de una muestra de sujetos, su estatura media podrá venir dada en centímetros, pero la varianza serán centímetros cuadrados. No podemos mezclar unidades de longitud con unidades de superficie. La solución ahora es inmediata, la raíz cuadrada de la varianza será una medida de dispersión basada en un promedio y que ahora sí tendrá las unidades originales de la variable. Esta medida, es la desviación típica o desviación estándar, cuya expresión viene dada por
\[s=\sqrt{\sum_{i=1}^{n}{\frac{(xi-\bar{x})^2}{n-1}}}. \tag{4.8}\]
Observemos que esta definición es la dada para una media cuadrática en la Sección 4.3.1.3. Efectivamente, la desviación típica es la media cuadrática de las distancias de cada observación a la media aritmética, solo que en el denominador se consideran los grados de libertad (\(n-1\)), y no el número total de observaciones (\(n\)), debido a que hay presente una restricción.
4.3.2.4 Coeficiente de variación
Dos desviaciones típicas no se pueden comparar si no aluden a dos distribuciones de la misma variable que tengan la misma media. En la práctica, esto no suele encontrarse, pero se puede combinar la información que aportan la desviación típica y la media para construir el coeficiente de variación
\[CV=\frac{s}{\bar{x}}\cdot 100\%.\] Este coeficiente, que expresa la desviación típica en unidades de media, es una medida adimensional que habitualmente se multiplica por 100 y se expresa como porcentaje. Al no tener dimensiones, este coeficiente permite comparar la variabilidad de distribuciones con diferente media pero incluso con diferentes unidades de medida.
Una aplicación frecuente del \(CV\) se la cuantificación del error de medida de un instrumento. Se mide repetidamente y en las mismas condiciones el mismo objeto y la variabilidad de las medidas obtenidas constituye el error de medida, que puede expresarse en términos porcentuales de acuerdo a este coeficiente.
No es una medida que se pueda obtener siempre. Si \(\bar{x}<0\) el coeficiente será negativo y una medida de dispersión negativa carece de sentido. Aunque hay autores que definen a este coeficiente como , no es la opción por la que optamos aquí. Obviamente, si \(\bar{x}=0\) la división por cero genera una indeterminación matemática y el coeficiente no está definido. Pero tampoco es una medida robusta si la media es pequeña. Un denominador próximo a cero da lugar a un cociente inestable que puede amplificar excesivamente una pequeña variación en el mismo. Así que la recomendación es que este coeficiente solo es procedente si \(\bar{x}>1\).
Conviene señalar que, en distribuciones con alta variabilidad, el coeficiente de variación puede ser superior al 100%.
El coeficiente inverso, \(\frac{\bar{x}}{s}\), se denomina en ingeniería coeficiente señal-ruido (Peña Sánchez de Rivera (2014)).
4.3.2.5 Rango intercuartílico
Cuando se utiliza la mediana para sintetizar la posición central de la distribución, no parece muy adecuado utilizar como medida de dispersión a la desviación típica, que en su definición implica como medida de posición a la media aritmética. En este caso, las medidas de posición mas comunes se basan en los cuartiles.
El rango intercuartílico se define como la diferencia entre el tercer y el primer cuartil \[RIQ=Q_3-Q_1.\] Este valor refleja en cuántas unidades de la variable se distribuye el 50% central de las observaciones. Por ejemplo, si en la puntuación de un cuestionario que puede tener 20 puntos como máximo, se observa que \(Q_1=12\) y \(Q_3=16\), entonces \(RIQ=16-12=4\). Es decir, el 50% central de las puntuaciones se distribuyen en 4 unidades de recorrido de la variable.
Una medida similar es el rango semi-intercuartílico, que viene definido como \(RSI=\frac{RIQ}{2}\). En el ejemplo anterior, este valor sería de 2 unidades. Pero eso no implica que el 25% central (superior o inferior) se distribuya en esas 2 unidades, será así siempre que la distribución sea simétrica, al menos en su parte central.
También es posible definir una medida de variación relativa, similar al coeficiente de variación, basada en cuartiles. Para ello, se considera el \(RSI\) como medida de dispersión, y el punto medio entre el primer y el tercer cuartil, esto es \(\frac{1}{2}(Q_1+Q3)\), como medida de posición. Este punto medio deberá ser próximo a la mediana cuando la distribución sea simétrica (al menos en la parte correspondiente al 50% central de los datos). Se tiene así el coeficiente de variación cuartílica \[V_Q=\frac{Q_3-Q_1}{Q_3+Q_1}\cdot100\%\]
4.3.3 Posición y dispersión, dos tipos de medidas inseparables
Al sintetizar mediante medidas descriptivas la distribución de una variable, debe indicarse al menos una medida de posición acompañada de una de dispersión. Ninguna de estas medidas representa gran cosa de forma aislada, debiendo venir cada una acompañada de la otra. En este sentido, la pareja de medidas más habitual es la formada por la media y la desviación típica. En muchos textos puede verse esta información con el formato \(m \pm s\), en donde \(m\) es la forma de aludir a la media aritmética (en lugar de \(\bar{x}\)) en ámbitos de tipo aplicado, en donde se usa menos simbología matemática. Hay que aclarar que la expresión anterior es solo una forma de notación. En general no se pretende aludir a un intervalo, aunque de manera estricta, es lo que está representando. Para evitar esta inducción a confusión, la American Psychological Asociation (APA), una entidad que publica un manual de estilos para los textos científicos de reconocido prestigio internacional, recomienda evitar el uso del símbolo \(\pm\) y en su lugar escribir \(m\; (s)\). Por ejemplo, si la edad observada en una muestra tiene una media de 37 años y una desviación típica de 10 años, la forma de expresar esta información sería \(37\, (10)\;\) años. Por cierto, en estas expresiones hay que utilizar un número de decimales coherente (¿tiene sentido expresar una variable como los años de edad con dos o tres decimales? ¿aporta alguna información de valor ese exceso de decimales?). Por otra parte, la desviación típica siempre debe estar expresada con los mismos decimales que la media, o uno más, nunca menos.
La información conjunta que proporcionan la media y la desviación típica queda establecida por la desigualdad de Tchebychev, que establece que entre la media y \(k\) veces la desviación típica se acumula, al menos, el \[(1-\frac{1}{k^2})\cdot 100\%\] de las observaciones. En Peña Sánchez de Rivera (2014) puede verse la demostración de esta importante propiedad, que se verifica para cualquier tipo de distribución.
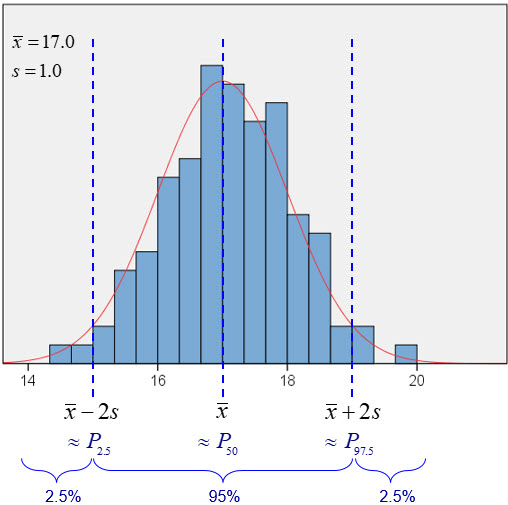
Cuando la distribución es simétrica y con forma de campana (más adelante, en la sección ??, llamaremos a este tipo de distribución normal), se puede precisar mejor la proporción de casos que queda comprendida entre la media y \(k\) veces la desviación típica. Concretamente, en este tipo de distribución, en el intervalo \(\bar{x}\pm s\) se encuentra, aproximadamente, el 95% central de la distribución (Figura 4.15). Es decir, que \(\bar{x}-2\, s\;\approx\;P_{2.5}\) y \(\bar{x}+2 \, s\;\approx\;P_{97.5}\).
Como ya se ha indicado, en el caso de sintetizar la posición central de la distribución con la mediana, la medida de dispersión acompañante suele ser el rango intercuartílico o también el semiintercuartílico. Obsérvese, que la mediana no tiene por que ser equidistante de los cuartiles primero y tercero, esto solo ocurre cuando la distribución es simétrica, al menos en su 50% central.
4.3.4 Cálculo de las medidas descriptivas con el sistema base de R
Las siguientes funciones admiten la especificación del parámetro na.rm, que alude a eliminar los casos faltantes (not_available.remove) antes de aplicar la función en cuestión. Su valor por defecto es na.rm = FALSE, lo que provoca que la función se interrumpa (no se calcula) cuando aparecen casos con valores faltantes <NA> . Estableciendo na.rm = TRUE se excluyen los casos con información faltante del cálculo.
Funciones para obtener las medidas descriptivas
Tablas de frecuencias
table(variable)proporciona una tabla con las frecuencias absolutas de cada categoría o valor de la variable indicada.
Medidas de posición
median(variable)mediana.mean(variable)media aritmética.weighted.mean(variable,ponderación)Media ponderadamin(variable)valor mínimo de la distribución.max(variable)valor máximo de la distribución.quantile(variable, \(\alpha\))proporciona el percentil \(\alpha\) de la variable.
Medidas de dispersión
var(variable)varianza.sd(variable)desviación típica.IQR(variable)recorrido, o rango intercuartílico.- El coeficiente de variación. No está implementado en el lenguaje base, pero se obtiene fácilmente a través de la expresión
sd(variable)/mean(variable)
Otras funciones descriptivas
summary(variable)proporciona una tabla con los extremos, los tres cuartiles y la media de la distribuión.
4.3.5 Funciones descriptivas en BioestadisticaR2
El paquete BioestadisticaR implementa dos funciones de tipo descriptivo freq() y grps()
BioestadisticaR2: Funciones descriptivas.
freq(), que permite obtener la tabla de frecuencias absolutas y relativas de las categorías de una variable. Si la variable es cuantitativa permite realizar su agrupación en intervalos. Sus argumentos son:xvector o data.frame a describir. Si se indica un data.frame proporciona una salida para cada una de sus variables.acumvalor lógico, si es TRUE proporciona la frecuencia relativa acumuladacutsvalor entero que permite indicar el numero de intervalos a realizar. Si se omite se utiliza el criterio de Sturges.agrupvalor lógico. Por defecto, se realiza automáticamente la agrupación en intervalos de aquellas variables que tengan más de 10 valores distintos. Si se estableceagrup=FALSEno se hace agrupación (aunque haya más de 10 categorías).decsvalor entero. Permite especificar el número de decimales a mostrar en la salida. Por defecto este valore es de tres.grfvalor lógico. Si esTRUE(FALSE) se proporciona(omite) la salida gráfica. Por defecto esTRUE
Para obtener el recuento, la media y la desviación típica de una variable segmentada por los niveles de un factor, el paquete implementa la función
grps(variable, factor)proporciona una tabla con la media y desviación típica de la variable indicada para cada grupo establecido por los niveles de factor.
BioestadísticaR2: Ejemplos de las funciones descriptivas.
A continuación se presentan algunos ejemplos del uso de estas funciones.
dat<-c(12,15,13,12,11,14,15,15,15,12,11,13,14,15,NA)
BioestadisticaR2::freq(dat,grf=FALSE)
Distribución de frecuencias
--------------------------------
Variable: dat
Valores faltantes: 1
n= 14
x Freq Prop Prop.Acum
1 11 2 0.143 0.143
2 12 3 0.214 0.357
3 13 2 0.143 0.500
4 14 2 0.143 0.643
5 15 5 0.357 1.000sexo <- factor(c("hombre","hombre","mujer","hombre","mujer","mujer","mujer","hombre","mujer","hombre"),levels=c("mujer","hombre"))
calcio <- c(9.8,9.5,8.7,10.2,9.3,9.6,8.9,10.4,9.9,10.2)
BioestadisticaR2::grps(calcio, sexo, grf=FALSE)
# Descriptiva de calcio por sexo
# ------------------------------
sexo
n media dt
mujer 5 9.280 0.492
hombre 5 10.020 0.363
Total 10 9.650 0.564En los dos ejemplos se ha indicado grf=FALSE para no alargar este documento, si deja esta opción en TRUE podrá ver el diagrama resultante en el panel de gráficos de RStudio.
Matemáticamente, la distancia entre dos puntos se obtiene como su diferencia. Por ejemplo, la distancia entre 7 y 10 es de 10-7=3 unidades.↩︎